Terminale
Spécialité
Limites de suites
Suites géométriques, suites monotones

Suites géométriques, suites monotones

Suites du type (qn)(q^n)

Propriétés

Soit qq un réel.

  • Si q≤−1q \leq -1 alors la suite (qn)(q^n) diverge et n’admet pas de limite.
  • Si −1<q<1-1 < q < 1 alors la suite (qn)(q^n) converge vers 0.
  • Si q=1q = 1 alors la suite (qn)(q^n) converge vers 1.
  • Si q>1q > 1 alors la suite (qn)(q^n) diverge vers +∞+\infty.
Exemples

  • Soit un=2nu_n = 2^n pour tout n∈Nn \in \mathbb{N}.
    2>12 > 1 donc, d’après la propriété, lim⁡n→+∞2n=+∞\lim\limits_{n \to +\infty} 2^n = +\infty.
    D’où lim⁡n→+∞un=+∞\lim\limits_{n \to +\infty} u_n = +\infty.

  • Soit vn=(13)nv_n = \left(\dfrac{1}{3}\right)^n pour tout n∈Nn \in \mathbb{N}.
    −1<13<1-1 < \dfrac{1}{3} < 1 donc, d’après la propriété, lim⁡n→+∞(13)n=0\lim\limits_{n \to +\infty} \left(\dfrac{1}{3}\right)^n = 0.
    D’où lim⁡n→+∞vn=0\lim\limits_{n \to +\infty} v_n = 0.

Remarque

Ce théorème permet en particulier de conclure sur la convergence ou la divergence d’une suite géométrique et d’en calculer la limite éventuelle.

Suites monotones

Soit (un)(u_n) une suite de nombres réels. Soient MM et mm deux réels.

Théorème (admise)

  • Si (un)(u_n) est croissante et majorée, alors (un)(u_n) converge.
  • Si (un)(u_n) est décroissante et minorée, alors (un)(u_n) converge.

Corollaire

  • Si (un)(u_n) est croissante et majorée par MM, alors (un)(u_n) converge vers une limite ℓ\ell telle que ℓ≤M\ell \leq M.
  • Si (un)(u_n) est décroissante et minorée par mm, alors (un)(u_n) converge vers une limite ℓ\ell telle que ℓ≥m\ell \geq m.

Remarque

Le théorème assure de l’existence de la limite ℓ\ell de la suite mais il ne donne pas la valeur de cette limite.
Le corollaire précise que si la suite est majorée par MM, alors ℓ≤M\ell \leq M.
Par exemple, pour la suite représentée ci-dessous, 3.53.5 (en pointillé) est un majorant mais n’est pas la limite.

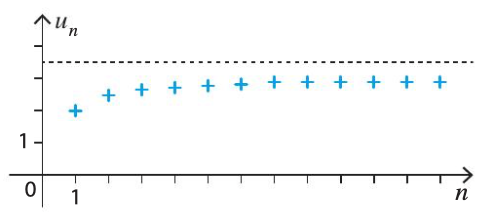
Théorème

  • Si (un)(u_n) est croissante et non majorée, alors (un)(u_n) diverge vers +∞+\infty.
  • Si (un)(u_n) est décroissante et non minorée, alors (un)(u_n) diverge vers −∞-\infty.

Théorème du point fixe

Théorème du point fixe

Si la suite (un)(u_n) converge vers ll et si la fonction ff est continue en ll, alors :

lim⁡n→+∞f(un)=f(l). \lim_{n \to +\infty} f(u_n) = f(l).


Soit (un)(u_n) une suite définie par la relation de récurrence : un+1=f(un)u_{n+1} = f(u_n).
Si on montre que (un)(u_n) converge (soit parce qu’elle est décroissante et minorée ou croissante et majorée) et si ff est continue, alors la limite ll vérifie :

l=f(l). l = f(l).


En pratique, on cherche à résoudre l’équation x=f(x)x = f(x) (c’est-à-dire l’intersection entre la courbe de la fonction et la droite y=xy = x) pour trouver les éventuelles limites.
Si deux limites existent, un raisonnement simple permet d’en éliminer une.

Déterminer la limite d’une suite du type (qn)(q^n)

Méthode 1 — Déterminer la limite d’une suite du type (qn)(q^n)

Déterminer la limite des suites ci-dessous, définies pour tout entier naturel nn.

  1. un=12nu_n = \dfrac{1}{2^n}
  2. vn=5n3nv_n = \dfrac{5^n}{3^n}
Solution commentée

1. Pour tout entier naturel nn,

un=12n=(12)n. u_n = \dfrac{1}{2^n} = \left(\dfrac{1}{2}\right)^n.

Or −1<12<1-1 < \dfrac{1}{2} < 1, donc

lim⁡n→+∞(12)n=0. \lim_{n \to +\infty} \left(\dfrac{1}{2}\right)^n = 0.

D’où lim⁡n→+∞un=0\lim\limits_{n \to +\infty} u_n = 0.

2. Pour tout entier naturel nn,

vn=5n3n=(53)n. v_n = \dfrac{5^n}{3^n} = \left(\dfrac{5}{3}\right)^n.

Or 53>1\dfrac{5}{3} > 1, donc

lim⁡n→+∞(53)n=+∞. \lim_{n \to +\infty} \left(\dfrac{5}{3}\right)^n = +\infty.

D’où lim⁡n→+∞vn=+∞\lim\limits_{n \to +\infty} v_n = +\infty.

Étudier la convergence d’une suite géométrique

Méthode 2 — Étudier la convergence d’une suite géométrique

Étudier la convergence de chacune des suites suivantes définies sur N\mathbb{N}.

  1. (wn)(w_n), suite géométrique de raison −53-\dfrac{5}{3} et de premier terme égal à 5.
  2. (zn)(z_n), suite géométrique de raison ee et de premier terme égal à −2-2.
Solution commentée

1. Pour tout n∈Nn \in \mathbb{N},

wn=5×(−53)n. w_n = 5 \times \left(-\dfrac{5}{3}\right)^n.

Or −53<−1-\dfrac{5}{3} < -1, donc, d’après le théorème du cours, (−53)n\left(-\dfrac{5}{3}\right)^n n’admet pas de limite.
Donc la suite (wn)(w_n) diverge et n’admet pas de limite.

2. Pour tout n∈Nn \in \mathbb{N},

zn=−2×en. z_n = -2 \times e^n.

Or e>1e > 1, donc, d’après le théorème du cours,

lim⁡n→+∞en=+∞. \lim_{n \to +\infty} e^n = +\infty.

Et, par produit,

lim⁡n→+∞zn=−∞. \lim_{n \to +\infty} z_n = -\infty.

La suite (zn)(z_n) diverge donc vers −∞-\infty.

Prouver la convergence d’une suite monotone

Méthode 3 — Prouver la convergence d’une suite monotone

Soit la suite (un)(u_n) définie par u0=4u_0 = 4 et, pour tout entier naturel nn,

un+1=12un+1. u_{n+1} = \tfrac{1}{2} u_n + 1.
  1. Montrer par récurrence que la suite (un)(u_n) est minorée par 2.
  2. En déduire que la suite (un)(u_n) est décroissante.
  3. Que peut-on en déduire pour la convergence de la suite (un)(u_n) ?
Solution commentée

1. Pour tout entier naturel nn, on considère la propriété P(n):un≥2P(n) : u_n \geq 2. On raisonne par récurrence.

  • Initialisation. Pour n=0n=0, u0=4u_0 = 4 donc P(0)P(0) est vraie.

  • Hérédité. On considère un entier quelconque k≥0k \geq 0. On suppose que P(k)P(k) est vraie, c’est-à-dire uk≥2u_k \geq 2.

    Alors 12uk≥1\tfrac{1}{2}u_k \geq 1, donc 12uk+1≥2\tfrac{1}{2}u_k + 1 \geq 2, soit uk+1≥2u_{k+1} \geq 2. Donc P(k+1)P(k+1) est vraie. La propriété est héréditaire.

  • Conclusion. La propriété P(n)P(n) est vraie au rang 0 et héréditaire, donc elle est vraie pour tout entier n≥0n \geq 0.
    Donc, pour tout entier naturel nn, un≥2u_n \geq 2. La suite (un)(u_n) est minorée par 2.

2. Pour tout entier naturel nn,

un+1−un=12un+1−un=−12un+1. u_{n+1} - u_n = \tfrac{1}{2}u_n + 1 - u_n = -\tfrac{1}{2}u_n + 1.

Or un≥2u_n \geq 2, donc −12un≤−1-\tfrac{1}{2}u_n \leq -1, donc −12un+1≤0-\tfrac{1}{2}u_n + 1 \leq 0, soit un+1−un≤0u_{n+1} - u_n \leq 0.
Donc la suite (un)(u_n) est décroissante.

3. La suite (un)(u_n) est minorée et décroissante, donc elle est convergente, c’est-à-dire qu’elle admet une limite réelle que l’on note ℓ\ell.
Comme, pour tout entier naturel nn, un≥2u_n \geq 2, on peut conclure que ℓ≥2\ell \geq 2.

Limites et comparaisonExercices