Limites et comparaison
Limite infinie
Théorème
Soit un entier naturel.
Soient et deux suites telles que, pour tout , .
- Si , alors .
- Si , alors .
Exemple
Soit la suite définie par , pour tout .
Pour tout entier naturel , on a :
Or, .
Donc, d’après le théorème précédent, .
Limite finie
Théorème des gendarmes (admise)
Soit un entier naturel et soit un réel.
Soient , et trois suites telles que, pour tout , .
Si et convergent vers la même limite , alors converge aussi vers .
Le schéma suivant illustre le théorème des gendarmes :
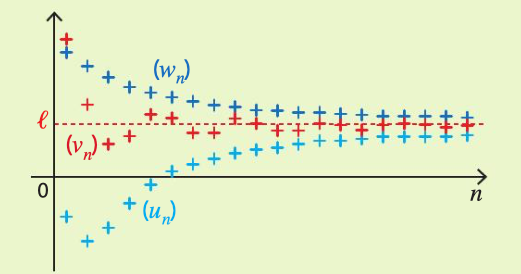
Remarque
Ce théorème permet simultanément de prouver que la suite converge et de déterminer la valeur de sa limite.
Il est aussi connu sous les noms de théorème d’encadrement ou théorème « sandwich ».
Propriété
Soit un entier naturel, soient et deux réels.
Soient et deux suites telles que, pour tout , .
Si converge vers et si converge vers , alors .
Propriétés
Soient un réel et une suite définie pour tout entier naturel .
- Si est croissante et converge vers , alors, pour tout , .
- Si est décroissante et converge vers , alors, pour tout , .
Déterminer une limite par comparaison
Méthode 1 — Déterminer une limite par comparaison
Déterminer la limite de chacune des suites définies ci-dessous.
- Pour tout , .
- Pour tout , .
Solution commentée
1. Pour tout , .
En ajoutant à chaque membre de l’inégalité, on obtient que, pour tout ,
ce qui équivaut à .
Or .
Donc, par comparaison, .
2. Pour tout , .
En ajoutant à chaque membre de l’inégalité, on obtient :
Donc , pour tout entier naturel .
Or , donc et, par somme, .
Donc, par comparaison, .
Déterminer la limite d’une suite avec le théorème des gendarmes
Méthode 2 — Déterminer la limite d’une suite avec le théorème des gendarmes
- Déterminer la limite de la suite , définie pour tout entier naturel tel que par :
- Étudier la convergence de la suite , définie pour tout entier naturel par :
Solution commentée
1. Pour tout entier naturel tel que , on a , d’où .
Or, la fonction inverse est strictement décroissante sur , donc pour tout entier naturel non nul :
soit
Or, et .
D’où, par passage à l’inverse :
D’après le théorème des gendarmes, on a donc .
2. Pour tout entier naturel , on a .
En ajoutant 2 à chaque membre de l’inégalité, on obtient :
Puis en divisant par , quantité positive, on a :
d’où :
Or, , donc, par passage à l’inverse :
Enfin, par somme :
D’après le théorème des gendarmes, on a donc : la suite converge et .