Définition des limites

Limite finie et suites convergentes

Définitions

Soit $\ell$ un réel. Une suite $(u_n)$ a pour limite $\ell$ quand $n$ tend vers $+\infty$ lorsque tout intervalle ouvert contenant $\ell$ contient tous les termes $u_n$ à partir d’un certain rang.
On dit alors que $(u_n)$ est convergente et converge vers $\ell$ .

Cette définition revient à dire que la suite $(u_n)$ converge vers $\ell$ lorsque, pour tout $r > 0$ , il existe un rang $N$ tel que pour tout $n \geq N$ , $|u_n - \ell| < r$ .

Remarque

$|u_n - \ell|$ représente la distance entre $u_n$ et $\ell$ .

Propriété

La limite d’une suite $(u_n)$ convergente est unique. On note $\lim\limits_{n \to +\infty} u_n = \ell$ .

Propriété (admise) : limites des suites usuelles

$\lim\limits_{n \to +\infty} \dfrac{1}{\sqrt{n}} = 0$ et $\lim\limits_{n \to +\infty} \dfrac{1}{n^k} = 0$ , où $k$ est un entier naturel non nul.

Le schéma suivant illustre la convergence d’une suite :

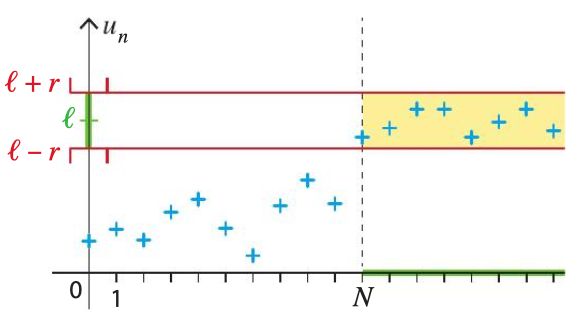
Suites divergentes

Définition

Une suite qui n’est pas convergente est dite divergente.

Définitions

Une suite $(u_n)$ tend vers $+\infty$ (respectivement vers $-\infty$ ) lorsque tout intervalle de la forme $[A ; +\infty[$ (respectivement de la forme $]-\infty ; A]$ ) contient tous les termes $u_n$ à partir d’un certain rang.
On note $\lim\limits_{n \to +\infty} u_n = +\infty$ (respectivement $\lim\limits_{n \to +\infty} u_n = -\infty$ ).
On dit alors que $(u_n)$ diverge vers $+\infty$ (respectivement vers $-\infty$ ).

Cette définition revient à dire que :

$(u_n)$ diverge vers $+\infty$ lorsque, pour tout réel $A$ , il existe un rang $N$ tel que pour tout $n \geq N$ , $u_n \geq A$ .
$(u_n)$ diverge vers $-\infty$ lorsque, pour tout réel $A$ , il existe un rang $N$ tel que pour tout $n \geq N$ , $u_n \leq A$ .

Remarque

Certaines suites divergent et n’ont pas de limite, par exemple la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n = (-1)^n$ .

Propriété (admise) : limites des suites usuelles

$\lim\limits_{n \to +\infty} \sqrt{n} = +\infty$ et $\lim\limits_{n \to +\infty} n^k = +\infty$ , où $k$ est un entier naturel non nul.

Le schéma suivant illustre la divergence d’une suite :

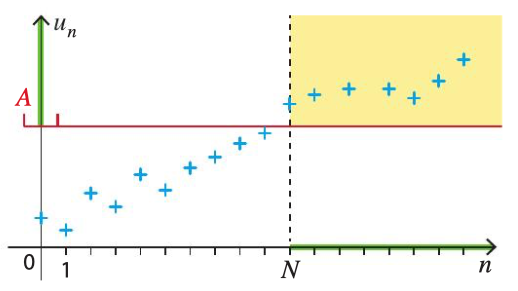
Déterminer une limite finie en utilisant la définition

Méthode 1 — Déterminer une limite finie en utilisant la définition

On s’intéresse à la suite $(u_n)$ , définie pour tout entier $n \geq 1$ par $u_n = 5 - \dfrac{1}{n}$ .

Recopier puis compléter le tableau ci-dessous.
$n$ 1 10 100 1000
$u_n$
$\lvert u_n - 5 \rvert$
Conjecturer le comportement de la suite $(u_n)$ quand $n$ tend vers $+\infty$ , puis justifier la conjecture en utilisant la définition de la limite d’une suite.

Solution commentée

$n$	1	10	100	1000
$u_n$	4	4,9	4,99	4,999
$\lvert u_n - 5 \rvert$	1	0,1	0,01	0,001

2. D’après le tableau, il semblerait que la suite $(u_n)$ converge vers 5.

Soit $r > 0$ . On cherche un rang $N$ à partir duquel $\left|5 - \dfrac{1}{n} - 5\right| < r$ , ce qui revient à $\dfrac{1}{n} < r$ .
C’est-à-dire, comme $n > 0$ , $1/n < r$ ou encore, par stricte décroissance de la fonction inverse sur $]0 ; +\infty[$ , $n > 1/r$ .

Donc, si l’on prend un entier $N$ supérieur à $1/r$ , on a, pour tout $n \geq N$ , $|u_n - 5| < r$ .

D’où $\lim\limits_{n \to +\infty} u_n = 5$ .

Déterminer une limite infinie en utilisant la définition

Méthode 2 — Déterminer une limite infinie en utilisant la définition

On s’intéresse à la suite $(v_n)$ , définie pour tout entier naturel $n$ par $v_n = 2 - 3n$ .

Recopier puis compléter le tableau ci-dessous.
$n$ 1 10 100 1000
$v_n$
Déterminer le plus petit rang $N$ tel que, pour tout $n \geq N$ , $v_n \leq -1000$ .
Conjecturer le comportement de la suite $(v_n)$ quand $n$ tend vers $+\infty$ , puis justifier la conjecture en utilisant la définition de la limite d’une suite.

$n$	1	10	100	1000
$v_n$

Solution commentée

$n$	1	10	100	1000
$v_n$	-1	-28	-298	-2998

2. $v_n \leq -1000$ équivaut à $2 - 3n \leq -1000$ , ou encore $n \geq \dfrac{1002}{3}$ , soit $n \geq 334$ .
Ainsi $N = 334$ .

3. D’après le tableau, il semblerait que la suite $(v_n)$ diverge vers $-\infty$ .

Soit $A$ un réel. On cherche un rang $N$ à partir duquel $2 - 3n \leq A$ , ce qui revient à $n \geq \dfrac{2 - A}{3}$ .

Donc, si l’on prend un entier $N$ supérieur à $\dfrac{2 - A}{3}$ , on a, pour tout $n \geq N$ , $v_n \leq A$ .

D’où $\lim\limits_{n \to +\infty} v_n = -\infty$ .

Limites et opérations