Notion de limite d’une suite

S’intéresser à la limite d’une suite $(u_n)$, c’est étudier le comportement des termes $u_n$ quand on donne à $n$ des valeurs entières aussi grandes que l’on veut, ce qui se dit aussi « quand $n$ tend vers $+\infty$ ».
Différents outils (calculatrice, tableur, Python…) fournissent une représentation graphique ou un tableau de valeurs de la suite qui permettent d’émettre différentes conjectures.

Limite finie

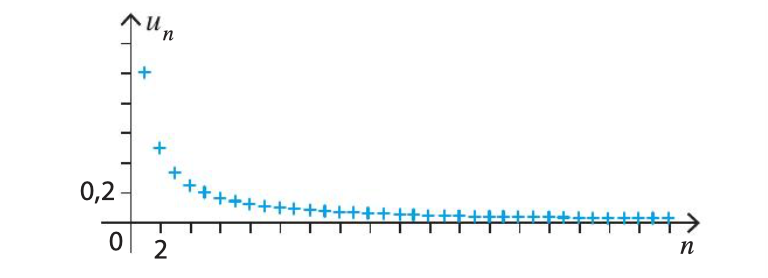
$(u_n)$ est définie par $u_n = \dfrac{1}{n}$, pour tout entier $n \geq 1$.

Les termes $u_n$ semblent se rapprocher autant que l’on veut d’une valeur « limite » : 0.
On dit que la suite $(u_n)$ tend vers 0 lorsque $n$ tend vers $+\infty$ et on note

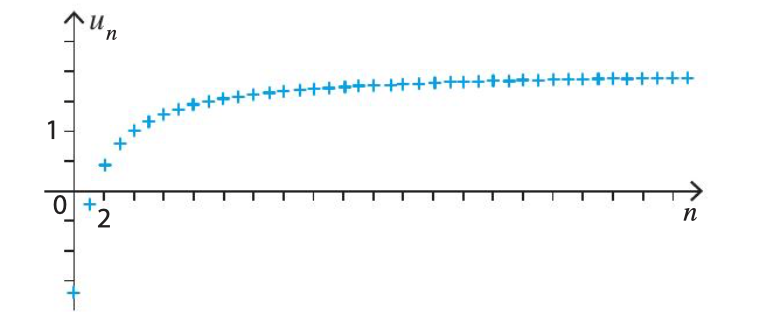
$(v_n)$ est définie par $v_n = \dfrac{4n-5}{2n+3}$, pour tout entier naturel $n$.

Les termes $v_n$ semblent se rapprocher autant que l’on veut d’une valeur « limite » : 2.
On dit que la suite $(v_n)$ tend vers 2 lorsque $n$ tend vers $+\infty$ et on note

Limite infinie

$(u_n)$ est définie par $u_n = n^2$, pour tout entier naturel $n$.

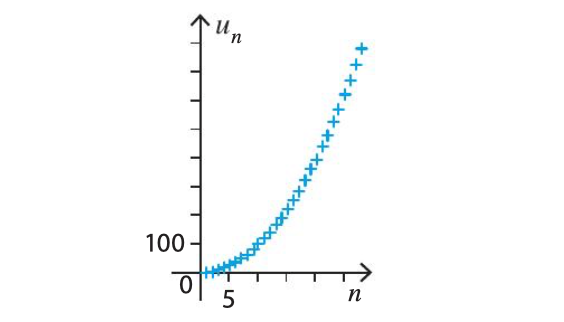
Les termes de la suite semblent devenir aussi grands que l’on veut.
On dit que $\lim_{n \to +\infty} u_n = +\infty$.

$(w_n)$ est la suite arithmétique de premier terme 16 et de raison $-2$.

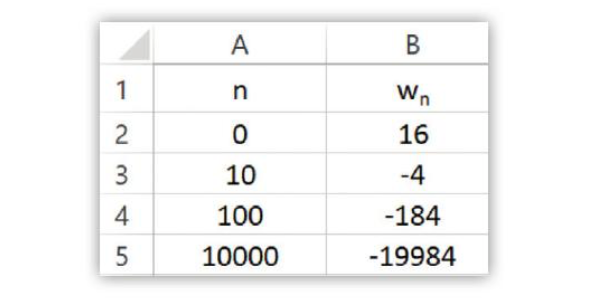
Les termes de la suite semblent devenir aussi grands que l’on veut en valeur absolue tout en étant négatifs.
On dit que $\lim_{n \to +\infty} w_n = -\infty$.

Pas de limite

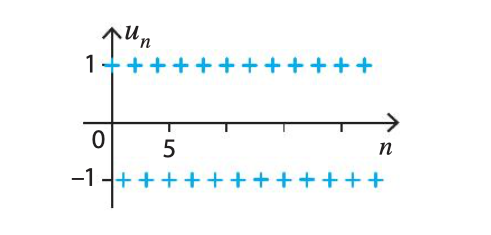
Il existe des suites qui n’ont pas de limite, comme la suite $(u_n)$ définie pour tout $n \in \mathbb{N}$ par $u_n = (-1)^n$.