Sens de variation d’une suite
Définition
Définition
On dit qu’une suite définie sur est :
- croissante si et seulement si, pour tout entier naturel , ;
- décroissante si et seulement si, pour tout entier naturel , ;
- constante si et seulement si, pour tout entier naturel , .
Remarques
- Pour certaines suites, l’inégalité n’est vraie que pour ; on dit que est croissante à partir du rang .
- Lorsqu’une suite est croissante ou décroissante, on dit qu’elle est monotone.
- Pour étudier le sens de variation d’une suite, on pourra étudier le signe de la différence de deux termes consécutifs .
Exemples
a. la suite des entiers naturels pairs est une suite croissante, chaque terme est supérieur au précédent.
b. La suite définie par n’est ni croissante ni décroissante. En effet, ses termes d’indices pairs sont égaux à 1 et ses termes d’indices impairs sont égaux à .
Cas d’une suite arithmétique de raison
Propriété
- Si alors la suite est strictement croissante.
- Si alors la suite est strictement décroissante.
- Si alors la suite est constante.
Cas particulier de la suite
Propriétés
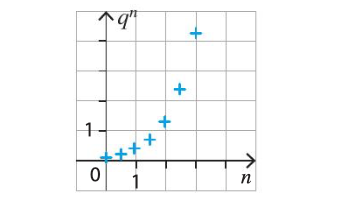
- Si alors la suite est croissante.
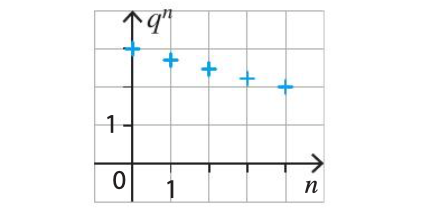
- Si alors la suite est décroissante.
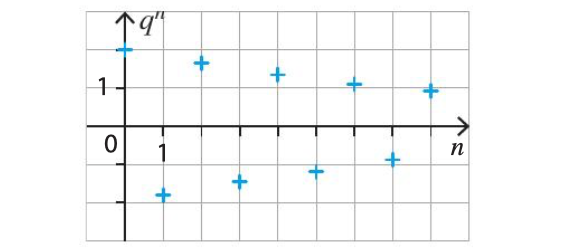
- Si alors la suite n’est pas monotone.
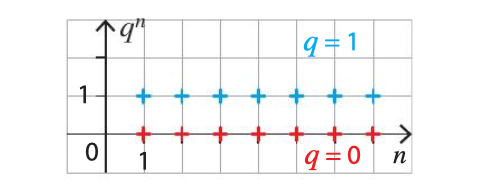
- Si , alors la suite est constante, à partir du rang 1.
- Si , alors la suite est constante, .
Remarque
Pour une suite géométrique de premier terme et de raison :
- si est positif, la suite a le même sens de variation que la suite ;
- si est négatif, la suite a le sens de variation contraire de celui de la suite .
Déterminer un sens de variation
Exercice résolu
- La suite est définie, pour tout entier naturel , par .
Montrer que est croissante. - La suite est définie, par
pour tout entier naturel .
Montrer que est décroissante.
Solution commentée
1. Pour tout ,
On en déduit que pour tout , , donc la suite est croissante.
2. Pour tout ,
On en déduit que pour tout , , donc la suite est décroissante.
Déterminer le sens de variation d’une suite arithmétique et d’une suite géométrique
Exercice résolu
Les suites et sont définies par :
pour tout entier naturel .
Déterminer la nature de chaque suite, puis déterminer son sens de variation.
Solution commentée
La suite est arithmétique de raison . Or est négatif, donc est décroissante.
La suite est géométrique de raison . Pour tout entier naturel ,
Or donc est décroissante. Comme est négatif, la suite est croissante.